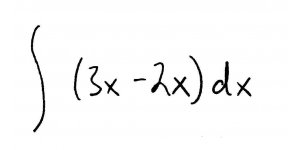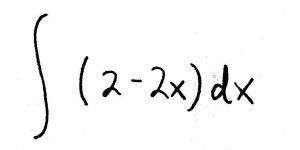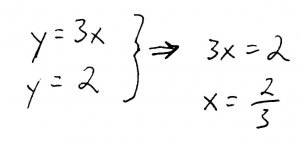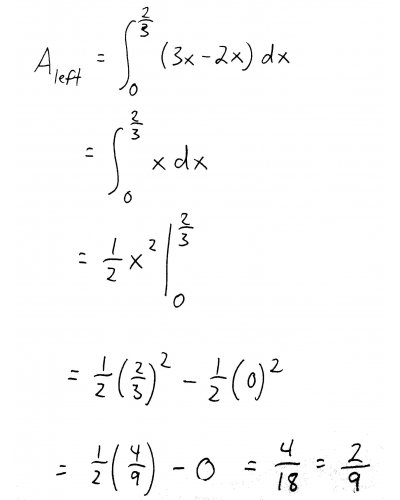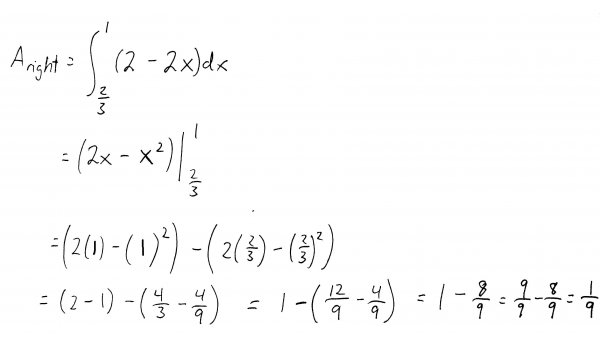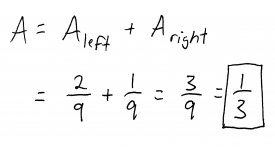Finding the area of (almost) any closed region

Howdy folks, Alex here! I thought I'd start this blog off right, with one of the most popular (and head-spinning) problems that get thrown at my calculus students. The problem goes something like this:

Find the area of the region enclosed by the lines \(y=2x\), \(y=3x\), and \(y=2\). You must use calculus or you will not receive any credit!

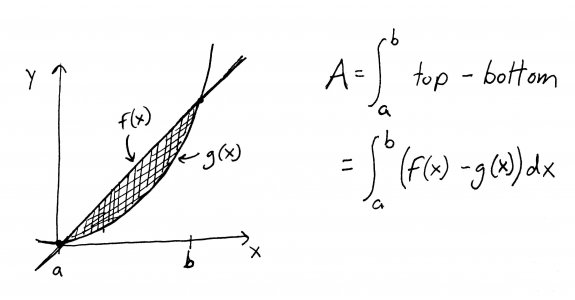
Whoa. Strong words from the guy with the gradebook. Alright, well hopefully you've already seen problems that ask for the area between two functions. If not, break out your textbook ;). The two-function area problems are solved by integrating the difference between the "top" and "bottom" functions, like so:

But wait a minute! Our problem is giving us THREE functions, not two. How in the name of Bieber can we apply the above formula to a region enclosed by three functions?

I'll tell you how. We're going to figure out a way to decompose, or break down, this difficult problem into several smaller, easier problems. Learning how to break down problems, by the way, is the reason that you are required to take calculus for your major - even if you'll never see another integral again in your entire life. Calculus is a great way to learn more general problem-solving skills, math or otherwise.

Ok, back to our problem. I'll repeat it here, since I've rambled quite a bit since I first stated it:

Find the area of the region enclosed by the lines \(y=2x\), \(y=3x\), and \(y=2\). You must use calculus or you will not receive any credit!

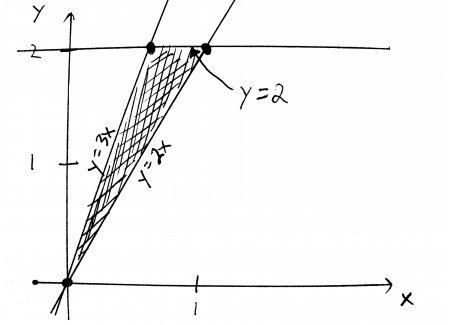
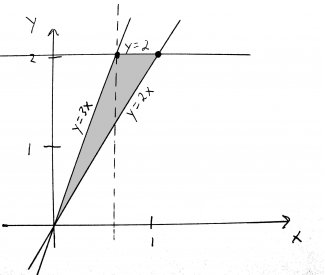
First, I want you to graph the lines, all on the same axes. I also want you to label the lines with their equations. Try to do it yourself before looking at my graph. HINT: you can graph any line by picking two different values of \(x\), plugging them into the equation to find the corresponding values of \(y\), plotting those two points, and drawing a straight line through them.

Looking at this picture, its not clear which function is the "top" function and which is the "bottom" function. Well, the line \(y=2\) looks the top function, and \(y=2x\) looks like the bottom function, but what about \(y=3x\)? Is it on top, on the bottom, or somewhere else entirely?

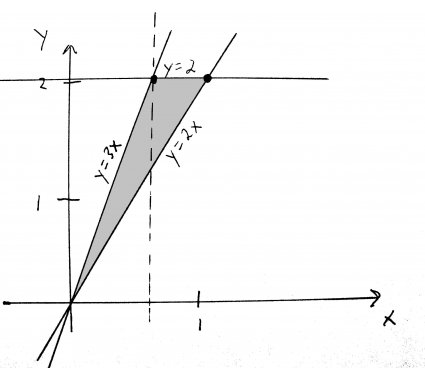
The answer is that \(y=3x\) is also on the top. Well, sometimes. Actually, it depends on which part of the triangle we're looking at. If we cut up this region at the point where \(y=3x\) and \(y=2\) intersect, the part that is to the left of the cut is bounded on top by \(y=3x\). The part to the right of the cut is bounded on top by \(y=2\). Let me show you what I mean:

I've drawn a dotted line to show where I cut the region. If you look at each piece separately, you will see that now they each have a distinct "top" and "bottom" function. That's hot. Now, we simply need to use the formula to find the area of each piece, and then add them together to get our final answer.

Ok, so the piece to the left of the dotted line is bounded on the top by \(y=3x\), and on the bottom by \(y=2x\). That gives us this integral:

The piece to the right of the dotted line is bounded on the top by \(y=2\), and on the bottom by \(y=2x\). That gives us the integral:

Great! We're ready to integrate, right? Hold it there, partner. The area formula requires a definite integral, and that means we need limits of integration (aka "bounds"). Well, remember that our boundaries are simply the values of \(x\) that tell us where the region begins and ends. To find them, lets look at the graph again:

Sweeping your eyes along the x-axis, the left piece starts at 0, and ends at the dotted line. What is the x-value at the dotted line, you might ask? Well, notice that it passes through the point where \(y=3x\) and \(y=2\) intersect. To find the x-value of this point, we simply set those two equations equal to each other, like so:

The right piece starts at the dotted line (which we've just found is at \(x=\frac{2}{3}\), and ends at 1. Why 1? Because its where the top and bottom functions intersect, thus closing off the region. We can show this mathematically by setting the equations of the top and bottom functions equal to each other:

Ok, now that we have our boundaries (0 to \(\frac{2}{3}\) for the left region, and \(\frac{2}{3}\) to 1 for the right region), we're ready to set up and solve our definite integrals. For the left piece, we get:

For the right piece, we get:

To get the area of the entire region, we simply add the areas of the individual pieces:

And there you have it. Not so bad, right? Like I said before, this problem is a great example of why we make business and biology students take calculus. Sure, you'll probably never have to find the area of a bounded region when you're dining with Gordon Gecko or curing cancer, but it teaches you how to tackle difficult problems by breaking them down into simpler pieces. And everyone faces a difficult problem in life sooner or later.