Optimization: using calculus to find maximum area or volume

Optimization, or finding the maximums or minimums of a function, is one of the first applications of the derivative you'll learn in college calculus.

In this video, we'll go over an example where we find the dimensions of a corral (animal pen) that maximizes its area, subject to a constraint on its perimeter. Other types of optimization problems that commonly come up in calculus are:

• Maximizing the volume of a box or other container
• Minimizing the cost or surface area of a container
• Minimizing the distance between a point and a curve
• Minimizing production time
• Maximizing revenue or profit

This video goes through the essential steps of identifying constrained optimization problems, setting up the equations, and using calculus to solve for the optimum points.

Review problem - maximizing the volume of a fish tank

You're in charge of designing a custom fish tank. The tank needs to have a square bottom and an open top. You want to maximize the volume of the tank, but you can only use 192 square inches of glass at most. What are the dimensions of the tank?

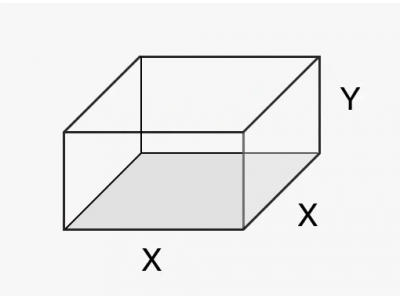
Step 1: Draw a picture and label the sides with variables

Step 2: Create your objective function and constraint equation

The objective function is the formula for the volume of a rectangular box:

\[ V = \text{length} \times \text{width} \times \text{height} = X \times X \times Y \\[2ex] V = X^2Y\]

The constraint equation is the total surface area of the tank (since the surface area determines the amount of glass we'll use). The surface area is simply the sum of the areas of the sides and bottom (the top is open).

\[ SA = X \times X + XY + XY + XY + XY \\[2ex] SA = X^2 + 4XY = 192\]

Step 3: Rearrange constraint equation and substitute into objective function

\[ V = X^2 \times Y \\[2ex] SA = X^2 + 4XY = 192 \\ \quad \quad \quad - X^2 \quad \quad - X^2 \\[2ex] 4XY = 192 - X^2 \\[2ex] \frac{4XY}{4X} = \frac{192 - X^2}{4X} \\[2ex] Y = \frac {1}{4X} \times (192-X^2) \\[2ex] V = X^2 \times \frac{1}{4X} \times (192-X^2) \\[2ex] V = \frac{X^2}{4X} \times (192-X^2) \\[2ex] V = \frac{X}{4} \times (192-X^2) \\[2ex] V = \frac{1}{4} \times (192X - X^3)\]

Step 4: Take the derivative, set it equal to zero, and solve

\[ V' = \frac{1}{4} \times (192 - 3X^2) = 0 \\[2ex] V' = [\frac{1}{4} \times (192 - 3X^2)] \times 4 = 0 \times 4 \\[2ex] V' = 192 - 3X^2 = 0 \\ \phantom{V' = } - 192 \quad \quad - 192 \\[2ex] - 3X^2 = -192 \\[2ex] \frac{-3X^2}{-3} = \frac{-192}{-3} \\[2ex] X^2 = 64 \\[2ex] \sqrt{X^2} = \sqrt{64} \\[2ex] X = 8\]

Step 5: Check if the point X = 8 is a max, min, or saddle point

Test slope at \(X=7\)

\[ V'(7) = \frac{1}{4} \times (192 - 3(7)^2) \\[2ex] V'(7) = \frac{1}{4} \times (192 - 147) \\[2ex] V'(7) = \frac{1}{4} \times 45 \\[2ex] V'(7) = \frac{45}{4} = 11.25 \\[2ex]\]

Test slope at \(X=9\)

\[ V'(7) = \frac{1}{4} \times (192 - 3(9)^2) \\[2ex] V'(7) = \frac{1}{4} \times (192 - 243) \\[2ex] V'(7) = \frac{1}{4} \times -51 \\[2ex] V'(7) = \frac{-51}{4} = -12.75\]

Derivative goes from positive, to zero, to negative, so \(X = 8\) is a max

Step 6: Solve for Y

\[ Y = \frac {1} {4X} \times (192-X^2) \\[2ex] Y = \frac {1} {4 \times 8} \times (192-8^2) \\[2ex] Y = \frac {1} {32} \times (192-64) \\[2ex] Y = \frac {1} {32} \times (128) \\[2ex] Y = \frac {128} {32} \\[2ex] Y = 4\]

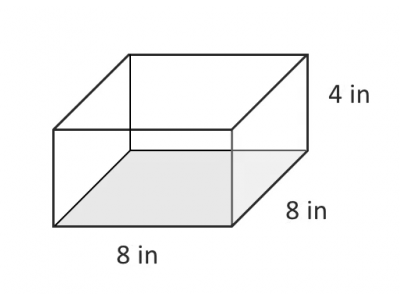
An \(8 \times 8 \times 4\) inch tank gives us the maximum volume.