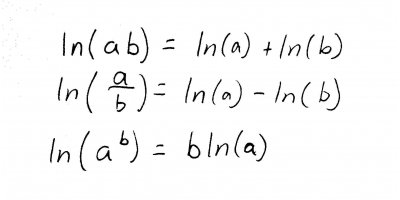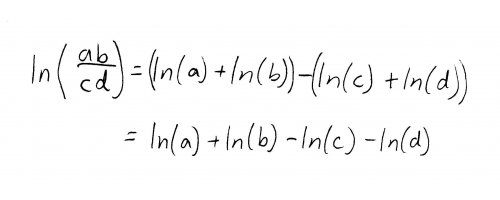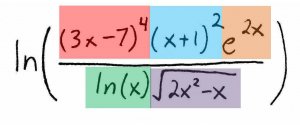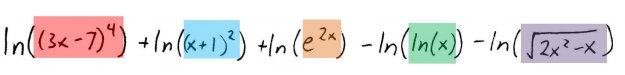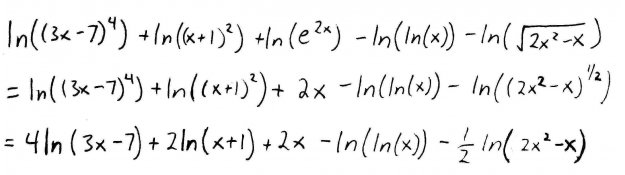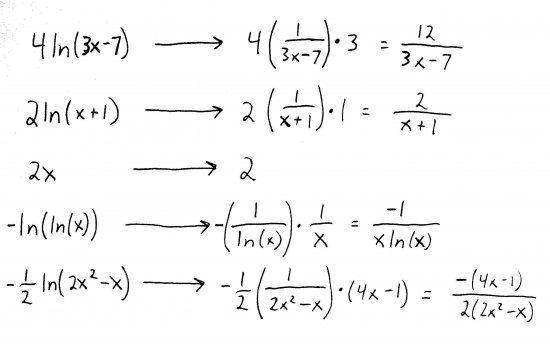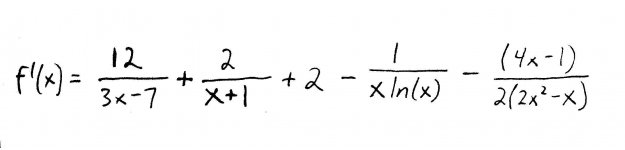An easier way to take the derivative of complicated logarithmic functions

Math can often feel overwhelming. Sometimes, it just looks overwhelming, even when you actually know how to do it. This visual intimidation factor is something that breeds anxiety, induces brain farts on tests, and ultimately turns a lot of people off to math. Case in point, our calculus problem this evening:

Example: Find the first derivative of:

\(f(x)=ln\left (\frac{(3x-7)^{4}(x+1)^{2}e^{2x}}{ln(x)\sqrt{2x^2-x}} \right )\)

Hint: There is an easy way, and a hard way to approach this problem. Use the easy way.

This function, frankly, looks terrifying. Its full of exponents and natural logs and square roots, all jammed up against one another in some night-before-the-test anxiety dream. The hint provides a glimpse of comfort, if only we can figure out the "easy way." If not, we'll be doing chain rules inside product rules inside quotient rules inside chain rules all night, run out of time, and probably fail the exam. Basically, if you see a problem like this and don't know the trick, you're better off skipping it entirely.

But let's not do that! The trick is to use the rules of logarithms to expand, or rewrite the function before we even mention the word "derivative." There, I said it. Just to briefly review the rules of logarithms (and \(ln\), which is a specific type of logarithm), the important ones are:

The first rule tells us how to expand the log of a product, the second the log of a quotient, and the third the log of a power. How do these help? Well notice that our problem consists of a logarithm of the product of factors in the numerator, divided by the product of some other factors in the denominator. We can define a compound logarithm rule that tells us how to approach situations like this, with multiple factors being multiplied and divided:

Notice that the factors in the numerator become logarithms that get added, and the factors in the denominator become logarithms that get subtracted. Now let's now take a look at the factors in our problem:

As you can see, we've got three factors in the numerator, and two in the denominator. Expanding this entire logarithm at once, we get:

Notice that the last two terms are negative, because their factors came from the denominator. We could stop here, but we can also further simplify by rewriting the square root in the last term as a rational exponent, using the logarithm-of-powers rule (the third one in our list of rules) on the first, second, and last term, and using the fact that \(ln\) and \(e\) are inverses of each other on the third term:

Ok. We've done everything we can (notice that the fourth term, which has a log inside of a log, can't be further simplified). Now, its time to take derivatives. This is going to be a lot easier to differentiate because we have a bunch of terms being added and subtracted instead of multiplied and divided. That means: goodbye, nasty product and quotient rules. We'll still need the chain rule, though, for the first two and last two terms. The chain rule for logarithms is just a special case of the chain rule you learned earlier in the semester. But in case its not immediately obvious, here it is:

Applying this rule to each term, we get:

Putting everything back together, we get our final answer:

Got it? This is just another example of how learning math gets us used to breaking down large, intimidating problems into several smaller, manageable problems. What could make life easier than that?