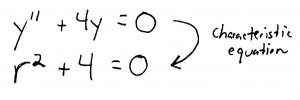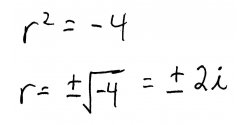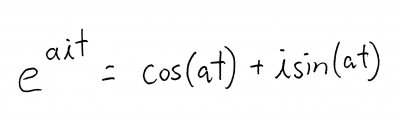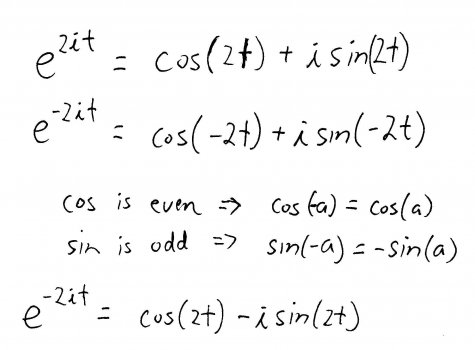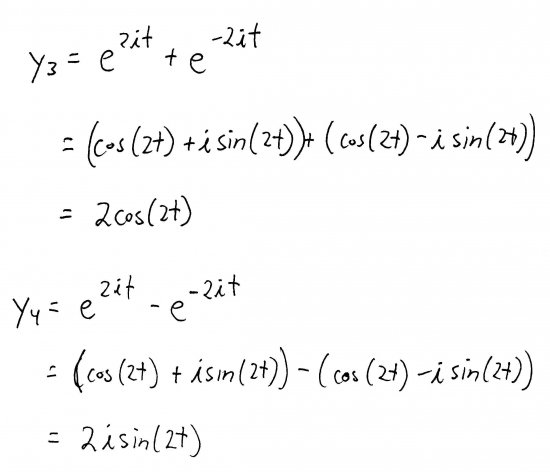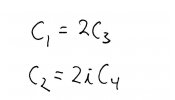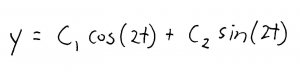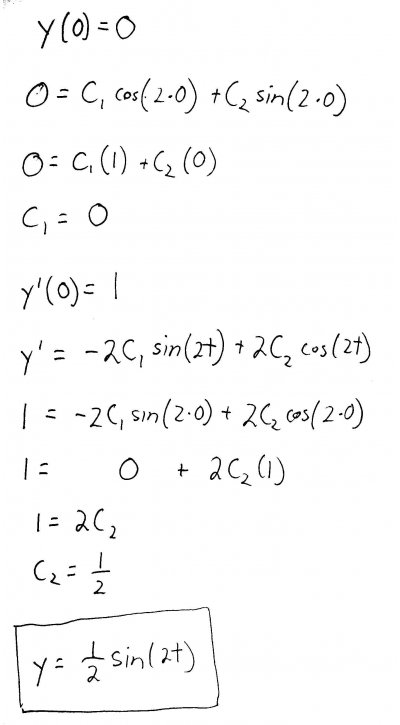Solving a second-order, homogeneous differential equation with complex roots

Or more specifically, a second-order linear homogeneous differential equation with complex roots. Yeesh, its always a mouthful with diff eq. Oh and, we'll throw in an initial condition just for sharks and goggles. The problem goes like this:

Find a real-valued solution to the initial value problem \(y''+4y=0\), with \(y(0)=0\) and \(y'(0)=1\). Your solution must be real-valued or you will not receive full credit!

If you'll recall, the steps for solving a second-order homogeneous diff. eq. are as follows:

1. Write down the characteristic equation.
2. Find the roots of the characteristic equation.
3. Use the roots to write down the two exponential basis solutions.
4. Create a general solution using a linear combination of the two basis solutions.

For step 1, we simply take our differential equation and replace \(y''\) with \(r^2\), \(y'\) with \(r\), and \(y\) with 1. Easy enough:

For step 2, we solve this quadratic equation to get two roots. The roots are going to be complex numbers, but that's ok:

Step 3 tells us to write down the resulting basis solutions using our two roots:

When we get to step 4 though, we have a problem. We're supposed to find a real-valued solution. Clearly, anything that has \(i\) in it is not real-valued. So, are we SOL on this one? Maybe not. It turns out that we can make a real-valued solution out of two non-real basis solutions using two tricks (and isn't diff. eq. all about tricks)?

Our first trick comes to us all the way from Switzerland via one Leonhard Euler (pronounced "Oiler"). Its called, naturally enough, Euler's Formula, and tells us how we can turn a complex exponential function into a complex trigonometric function. Don't worry about why it works, just know that the formula is:

Pretty cool, huh? The other trick we're going to use is the fact that any linear combination of solutions to a given linear differential equation is also a solution. In other words, we can slice and dice our solutions (by multiplying them by constants and adding them together) to get more solutions.

Obviously, we want to do our slicing and dicing in a way that lets us end up with a real-valued solution. But, exactly which way is not so obvious. So I'll show you, and you can more or less rely on this technique for similar types of problems. We're going to define two new solutions, one by adding our basis solutions, and one by subtracting them:

Using Euler's Formula, we can rewrite those exponential basis solutions in terms of trig functions. Recall that cosine is an even function and sine is an odd function, so we can do a bit of simplification with the negative root:

Plugging that into the equations for \(y_{3}\) and \(y_{4}\), we can simplify them and get two nice, clean, pretty new solutions:

Now, we can make a linear combination out of those solutions to get our general solution:

Ah, you might say, but what about that \(i\) in the second term? Well notice that now that it has been safely moved out to the front of the term, we can simply define new constant coefficients for the terms. After all, \(i\) may be non-real, but its still a constant. So, we define:

and get:

I know, cheap trick. But it works! Now that we have our real-valued, general solution, we can use the initial conditions to find \(C_1\) and \(C_2\) and get the solution to our initial value problem:

There you have it. As you might have expected from other experiences you've had with differential equations, there are a series of not-so-obvious tricks that you have to use to solve the problem. Your best bet exam-wise is to simply commit these tricks to memory, and practice applying them over and over to similar problems from your textbook.