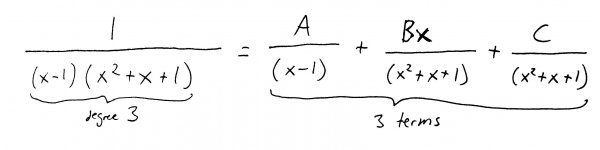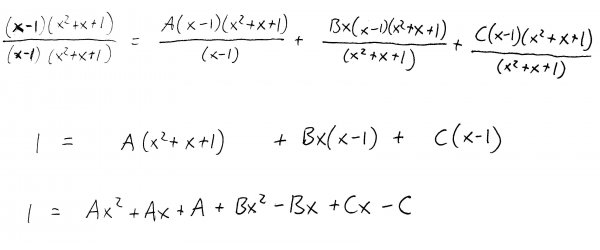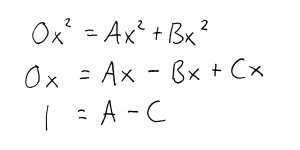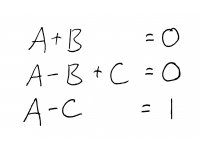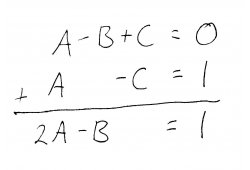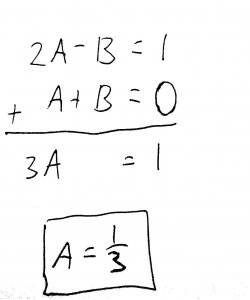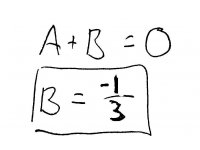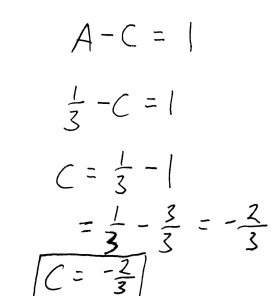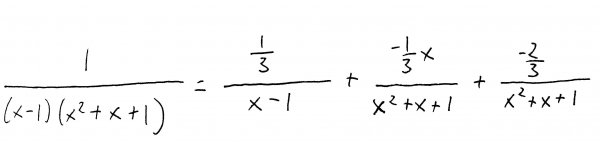The how and why of partial fraction expansion with unfactorable quadratics in the denominator

If you're reading this post, you've probably arrived at the point in your calculus course where they try to teach you how to do integration by partial fraction expansion. And if you're anything like I was when I first learned calculus, you're probably scratching your head and going whadafuhhhh? What is the point of all this?

Here's what you need to know. Partial fraction expansion is not an integration technique. It's an algebraic technique. That being said, it's useful for making certain algebraic expressions (i.e. rational expressions) easier to integrate by breaking them into smaller, simpler chunks. Sound familiar? Its that same mode of thinking that all your other calculus classes are pushing at - taking a difficult problem, decomposing it into several easier problems, and then putting the pieces back together.

Got it? Let's get down to business. Here's our problem:

Rewrite the following expression as the sum of three partial fraction terms: \[\frac{1}{(x-1)(x^2+x+1)}\]

Just to quickly review the steps (these should be in your textbook, or any online resource), the technique proceeds as follows:

1. Make sure that the degree of the denominator is greater than the degree of the numerator. If not, do the polynomial long division, and do the partial fraction expansion on any remainder that turns up. For our problem, the degree of the denominator is 3, and the degree of the numerator is 0, so we're good to go.
2. Factor the numerator and denominator of the expression (or remainder, if you got one in step 1), and cancel out any factors that the numerator and denominator have in common. Our problem is already as factored as its going to get. Notice that the quadratic term in the denominator can't be further factored.
3. Based on the factors in the denominator, write down the appropriate partial fractions with unknown coefficients in the numerator. The form of these terms is given in your textbook, and numerous other online resources, so I won't spell them out again here. Suffice it to say, our partial fraction expansion is going to look like this:

Now, you may be wondering why we have two different partial fractions corresponding to the same quadratic factor \((x^2+x+1)\). Also, why does one of those terms have an \(x\) in the numerator? The answer to both of those comes from a different course - linear algebra. Yes I know, you probably haven't taken that course yet, and its unfair, but that's life. I'll try to explain it the best I can:

In a nutshell, solving for the unknown coefficients (which we'll do in a moment) is going to give us a system of 3 linearly independent equations because the denominator of our expression is of degree 3. To get a unique solution, we thus need 3 unknown values: \(A\), \(B\), and \(C\). Furthermore, each partial fraction has to be linearly independent from the others. If we had simply written \(B\) instead of \(Bx\) in the second term, the second and third terms would add together and give us a single, combined constant in the numerator of \((x^2+x+1)\). Then, we'd be back where we started - we'd have only two (linearly independent) partial fractions, and thus no unique values for \(A\) and \(B\). Therefore, we always need one linearly independent partial fraction for each degree of the denominator.

Got it? To solve for \(A\), \(B\), and \(C\), we multiply both sides of the equation by the entire denominator of our original expression and simplify:

Next, we group like powers of \(x\) on the right-hand side of the equation and set them equal to corresponding powers of \(x\) on the left-hand side of the equation:

Dividing through by the corresponding powers of \(x\) in each equation, we get the following system of 3 equations with 3 unknowns:

Notice that if we didn't have the \(B\) term at all (i.e., if \(B = 0\)), then we would have gotten \(A = 0\) and then no possible solution for \(C\).

Now that we have this system of equations, we can solve it using any of the techniques for solving simultaneous equations. We could use either substitution or an elimination method alone, but I am going to use a hybrid approach by adding equations in such a way that eliminates one or more of the unknowns, and then substitute. Adding the second and third equations, we eliminate \(C\):

Now we can add this new equation to the first equation, eliminate \(B\), and solve for \(A\):

Plugging our value of \(A\) back into the first equation, we solve for \(B\):

And finally, plugging our value of \(A\) back into the third equation, we solve for \(C\):

So now we have found our coefficients: \(A=\frac{1}{3}\), \(B=-\frac{1}{3}\), and \(C=-\frac{2}{3}\). Plugging these back into our partial fraction terms, we get:

And there you have it. The right-hand side, our partial fraction expansion, makes it possible to do things we couldn't otherwise do with the original expression. For example, it would be impossible to directly integrate the original expression, but we know how to integrate these partial fraction terms. The first term can be integrated using a simple u-substitution, while the second and third terms would require completing the square and doing a trigonometric substitution (yuck!) Hey, no one said it would be easy, but at least now its possible.

The reason that partial fractions tend to give students so much trouble is that is brings together a whole bunch of different issues and techniques: polynomial long division, linear independence of functions, and solving systems of equations to name a few. On top of that, if the end goal is to integrate the expression, you might have to pull out all of the other integration techniques you've just learned in the past few weeks. The key with partial fraction problems is to take your time, carefully write down the correct form of the expansion, and then methodically work through finding the coefficients. Good luck!