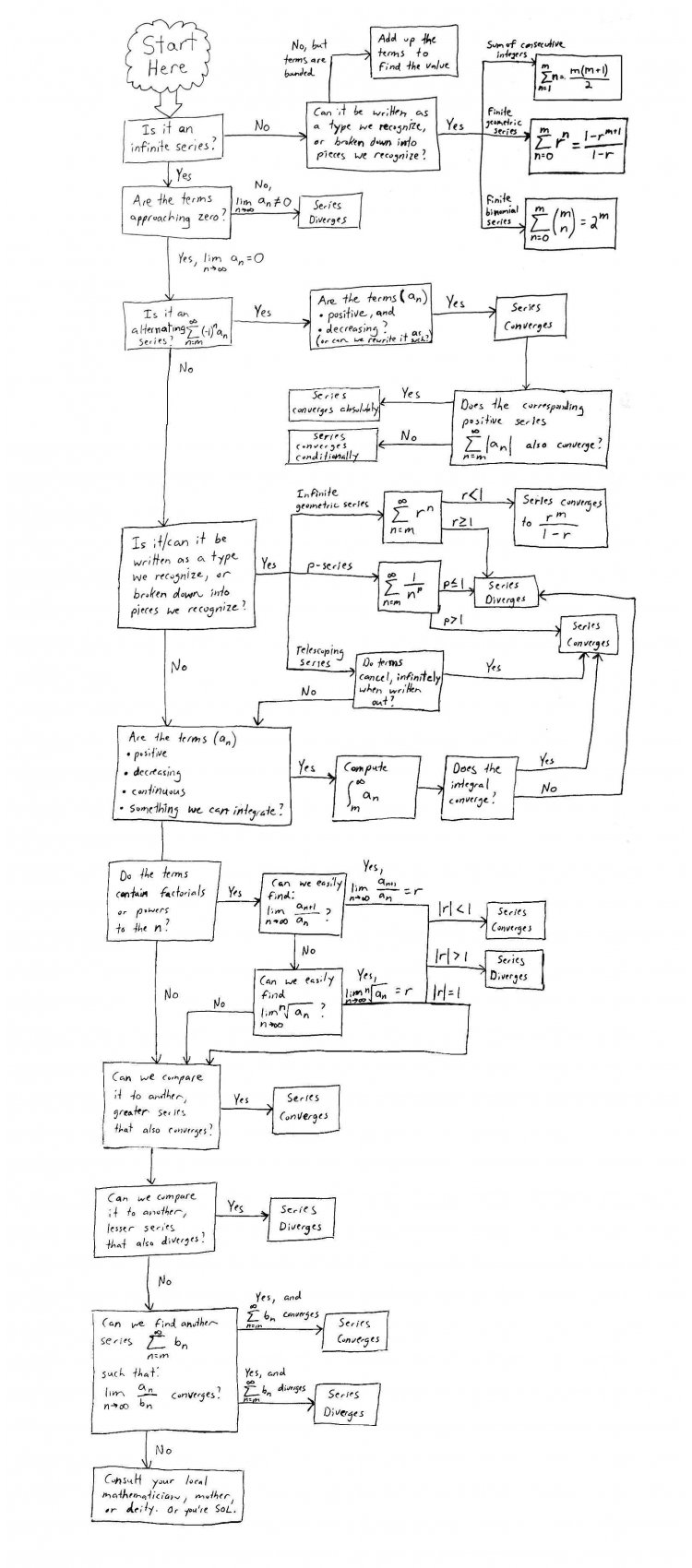
A flowchart for dealing with mathematical series

The chapter on series is notorious for making calculus students want to hurl their textbooks into a fire, curl up into a fetal position, and sob uncontrollably the night before the exam (I've been there myself).

Honestly, its not that series are so difficult as much as it requires you to remember a lot of rules, how to apply them, and most importantly, in what order to apply them. And most calculus courses just don't do all that great a job of explaining this - they just hurl a bunch of theorems at you, a few tests, and tell you to sort it all out yourself. To help with this, I've created a flowchart that explains how to approach solving a mathematical series. The important things to keep in mind are:

• There is a BIG difference between finite and infinite series. Look at the problem carefully before you decide how to approach it.
• Many tests are inconclusive about whether an infinite series converges/diverges. In that case, you must try another test.
• Just because we can prove that an infinite series converges, doesn't mean we can actually find the value that it converges to. You will only be expected to actually find the value of a relatively few convergent series - most notably, the infinite geometric series.
• Some times, the form of a series isn't quite apparent at first. You may need to use some nifty algebraic techniques, such as partial fractions, to get your series into a form you can work with.

Without further ado, here is the flowchart (click to enlarge). For more details on each type of series, consult your textbook or one of the many other fine resources available online.